Bruchrechnung
Im engeren Sinn bezeichnet Bruchrechnung das Rechnen mit gemeinen Brüchen (manchmal auch gewöhnlichen Brüchen) in der „Zähler-Bruchstrich-Nenner-Schreibweise“ (siehe unten). Bruchrechnung gehört damit zur Arithmetik, einem Teilgebiet der Mathematik.
In einem weiteren Sinn wird das Wort auch für das Rechnen mit rationalen Zahlen gebraucht, gleichgültig, in welcher Schreibweise sie vorliegen.
Eine wichtigere Erweiterung besteht in der Zulassung von Bruchtermen, das sind Ausdrücke, die formal wie gemeine Brüche gebildet werden, bei denen aber Zähler und Nenner Terme sein können, die Variablen enthalten. Für diese Bruchterme gelten die Bruchrechenregeln sinngemäß. Das Rechnen mit Bruchtermen gehört aber zur Algebra.
Die Regeln der Bruchrechnung beziehen sich auf die Grundrechenarten, also auf Addition, Subtraktion, Multiplikation, Division, sowie auf die Kehrwertbildung. Insbesondere bei Bruchtermen kommen auch Regeln für Potenzen und Wurzeln hinzu.
Außerdem gibt es eine Kürzungs- und Erweiterungsregel, die eine Besonderheit der Bruchrechnung ist. Sie beruht auf dem Unterschied zwischen Bruch und Bruchzahl, der im folgenden Abschnitt genauer dargestellt wird.
Die Bruchschreibweise, also die Schreibweise mit Bruchstrich, wird ganz allgemein in verschiedenen Bereichen der Mathematik, besonders in der Algebra, immer dann verwendet, wenn in der untersuchten Struktur die elementaren Bruchrechenregeln, insbesondere die Kürzungs- und Erweiterungsregel, gelten. Auch hier spricht man immer dann von „Bruchrechnung“, wenn diese Regeln angewendet werden.
Inhaltsverzeichnis
1 Bruch und Bruchzahl
2 Definition und Bezeichnungen
2.1 Gemeine Brüche
2.1.1 Echte und unechte Brüche
2.1.2 Stammbrüche und Zweigbrüche
2.1.3 Scheinbrüche
2.2 Gemischte Brüche
3 Rechenregeln
3.1 Praktisches Rechnen mit Brüchen
3.1.1 Formänderung von Brüchen
3.1.1.1 Umrechnen in eine Dezimalzahl
3.1.1.2 Erweitern und kürzen
3.1.1.3 Gemischte Zahlen einrichten und Ganze abspalten
3.1.1.4 Brüche gleichnamig machen
3.1.2 Die Grundrechenarten
3.1.2.1 Addieren und Subtrahieren
3.1.2.2 Multiplizieren
3.1.2.3 Dividieren
3.1.2.4 Rechnen mit gemischten Brüchen
3.2 Abstrakte Rechenregeln
3.2.1 Erweitern und Kürzen
3.2.2 Addition
3.2.3 Subtraktion
3.2.4 Multiplikation
3.2.5 Division
3.2.6 Potenzen
3.3 Rechnen mit Bruchtermen
3.3.1 Definitionsbereich
3.3.2 Kürzen
3.3.3 Addition und Subtraktion
3.3.4 Multiplikation und Division
4 Weitere Darstellungsformen
4.1 Partialbrüche
4.2 Ägyptische Brüche
4.3 Pythagoreische Brüche
4.4 Rationaler Zähler oder Nenner
5 Verallgemeinerungen
6 Siehe auch
7 Literatur
8 Weblinks
9 Einzelnachweise
Bruch und Bruchzahl

Die Bruchrechnung beruht darauf, dass sich das Ganze (die Eins aus dem Rechnen mit natürlichen Zahlen) noch unterteilen lässt. Einen Kuchen kann man zum Beispiel in vier Teile teilen. Wenn diese Teile gleich groß sind, so ist jedes Teil ein Viertel des Kuchens. Wenn, wie im Bild, eines der Viertel schon fehlt, so sind drei Viertel Kuchen dargestellt.
Das Ganze wird in vier gleiche Teile geteilt; drei davon sind hier gemeint. Oder: Drei Ganze werden gemeinsam in vier gleiche Teile geteilt; eines dieser gleichen Teile ist gemeint.
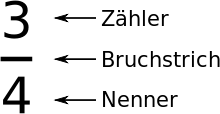
Geschrieben wird dies gewöhnlich in der „Zähler-Bruchstrich-Nenner-Schreibweise“: Die Zahl unter dem Bruchstrich, der Nenner gibt an, in wie viele Teile das Ganze geteilt worden ist; die Zahl über dem Bruchstrich, der Zähler gibt an, wie viele Teile davon in diesem Falle gemeint sind. So erhält man einen Bruch. Man kann diesen auch so deuten: Der Zähler gibt an, wie viele Ganze gemeinsam in soviele gleich große Teile zu teilen sind, wie der Nenner angibt. (Man legt drei Kuchen übereinander und teilt den Stapel in vier gleiche Teilstapel.)
Wird das Ganze (die Torte) stattdessen in acht Teile geteilt und werden davon sechs genommen, so ist das ein anderer Bruch: 68{displaystyle {frac {6}{8}}} statt 34{displaystyle {frac {3}{4}}}. Aber diese beiden Brüche stehen offenbar für die gleiche Menge Kuchen: Sie stehen für dieselbe Bruchzahl.
Für jede Bruchzahl gibt es viele (unendlich viele) verschiedene Darstellungen, verschiedene Brüche, die alle denselben Wert (dieselbe Größe) verkörpern, aber auf unterschiedliche Weise. Von einem Bruch zum anderen gelangt man durch Erweitern und Kürzen. Dadurch ändert sich der Wert einer Bruchzahl nicht, man erhält aber für diese Zahl verschiedene Darstellungsweisen: verschiedene Brüche.
Definition und Bezeichnungen
Brüche lassen sich zunächst in gemeine Brüche (auch gewöhnliche Brüche genannt) und Dezimalbrüche (= Dezimalzahl, umgangssprachlich: „Kommazahl“) einteilen, daneben gibt es noch die Darstellung als gemischter Bruch. Wenn man von einem Bruch spricht, meint man in der Regel einen gemeinen Bruch, das Rechnen mit Dezimalbrüchen wird meistens nicht als Bruchrechnung bezeichnet.
In der nachfolgenden Tabelle sind gebräuchliche Bezeichnungen für Brüche zusammengefasst, die in diesem Abschnitt erklärt werden. Die in der Tabelle weiter unten stehenden Begriffe fallen jeweils unter die darüberstehenden Oberbegriffe, zum Beispiel ist jeder Scheinbruch ein gemeiner Bruch, nebeneinanderstehende Begriffe müssen sich nicht ausschließen. Dabei ist zu beachten, dass es sich um Bezeichnungen für Zahlschreibweisen und nicht für die dargestellten Zahlen handelt. Eine bestimmte Zahl kann verschiedene Darstellungen haben, die jeweils mit unterschiedlichen Begriffen aus der Tabelle bezeichnet werden. So kann man zum Beispiel jeden unechten Bruch auch als gemischten Bruch schreiben.
| Bruch | ||||||
| gemeiner Bruch, gewöhnlicher Bruch | gemischter Bruch | Dezimalbruch | ||||
| echter Bruch, eigentlicher Bruch | unechter Bruch, uneigentlicher Bruch | |||||
| Stammbruch | Zweigbruch, abgeleiteter Bruch | Scheinbruch, uneigentlicher Bruch | unechter Bruch, der kein Scheinbruch ist | |||
Weitere Formen, in denen Bruchzahlen dargestellt werden können (Kettenbruch, Prozent- und Promilleschreibweise, Binärbrüche usw.) werden in je eigenen Artikeln behandelt und in dieser Tabelle nicht aufgeführt.
Gemeine Brüche

Beschreibung eines gemeinen Bruches
Gemeine Brüche werden im Allgemeinen durch eine Übereinanderstellung von Zähler und Nenner, getrennt durch einen waagerechten Strich, dargestellt:
- ZN{displaystyle {frac {Z}{N}}}
Zähler und Nenner eines Bruches sind ganze Zahlen. Dabei darf der Nenner N{displaystyle N} nicht null sein, da eine Division durch Null nicht definiert ist.
Jeder Bruch kann nämlich auch als Divisionsaufgabe verstanden werden. Dabei ist der Zähler Z{displaystyle Z} der Dividend, der Nenner N{displaystyle N} der Divisor:
- Z:N=ZN{displaystyle Z:N={frac {Z}{N}}}
Das Entscheidende bei der Bruchrechnung ist, dass hier jede Division (außer durch null) möglich ist und ein einfach darstellbares Ergebnis hat, während ja im Bereich der ganzen Zahlen die Teilbarkeitsregeln gelten.
Üblicherweise werden für Zähler und Nenner natürliche Zahlen verwendet und ein eventuell vorhandenes negatives Vorzeichen wird vor den Bruch gesetzt, also beispielsweise −34{displaystyle -{tfrac {3}{4}}} statt −34{displaystyle {tfrac {-3}{4}}} oder 3−4{displaystyle {tfrac {3}{-4}}}. Sind Zähler und Nenner negativ, so bezeichnet das nach den Regeln der Division von ganzen Zahlen den positiven Bruch: −3−4=34{displaystyle {tfrac {-3}{-4}}={tfrac {3}{4}}}
Bei einer Variante dieser Schreibweise, die oft verwendet wird, wenn gemeine Brüche in Texten vorkommen, werden Zähler, Bruchstrich und Nenner hintereinandergeschrieben und als Bruchstrich ein Schrägstrich verwendet,[1] zum Beispiel 1/2, 3/8. Bei der Schreibweise mit Schrägstrich an Stelle des waagrechten Bruchstrichs werden (vor allem) einstellige Zähler und Nenner manchmal verkleinert über bzw. unter den Schrägstrich geschrieben: 6/7. Zu diesem Zweck existieren in vielen Druckzeichensätzen Sonderzeichen, wie zum Beispiel ¾ oder ½.
Echte und unechte Brüche
Wenn bei einem Bruch der Betrag des Zählers kleiner als der des Nenners ist, dann spricht man von einem echten oder eigentlichen Bruch (z. B. 67{displaystyle {tfrac {6}{7}}} oder 25{displaystyle {tfrac {2}{5}}}), andernfalls von einem unechten oder uneigentlichen Bruch (z. B. 77{displaystyle {tfrac {7}{7}}} oder 113{displaystyle {tfrac {11}{3}}}).
Echte Brüche sind also die, deren Betrag kleiner ist als ein Ganzes.
Stammbrüche und Zweigbrüche
Ist der Zähler in einem gemeinen Bruch gleich 1 (z. B. 12{displaystyle {tfrac {1}{2}}} oder 19{displaystyle {tfrac {1}{9}}}), spricht man von einem Stammbruch, ansonsten von einem abgeleiteten Bruch oder Zweigbruch.
Scheinbrüche
Unechte Brüche, bei denen der Zähler ein ganzzahliges Vielfaches des Nenners ist (z. B. 123{displaystyle {tfrac {12}{3}}}), bezeichnet man als Scheinbrüche, da sie sich durch Kürzen in ganze Zahlen umwandeln lassen (im Beispiel in die Zahl 4). Insbesondere lässt sich jede ganze Zahl n{displaystyle n} als Scheinbruch n1{displaystyle {tfrac {n}{1}}} schreiben.
Gemischte Brüche
Unechte Brüche, die keine Scheinbrüche sind, lassen sich immer als gemischte Brüche (auch: als gemischte Zahlen, in gemischter Schreibweise) darstellen.
Dabei wird zunächst der ganzzahlige Anteil, d. h. die zur Null hin gerundete Zahl, geschrieben und anschließend direkt danach der verbleibende Anteil als echter Bruch. Zum Beispiel 113{displaystyle 1{tfrac {1}{3}}} statt 43{displaystyle {tfrac {4}{3}}} oder −335{displaystyle -3{tfrac {3}{5}}} statt −185{displaystyle -{tfrac {18}{5}}}.
Ein Problem der gemischten Schreibweise ist, dass sie als Produkt missverstanden werden kann:
So steht 213{displaystyle 2{tfrac {1}{3}}} meist für 2+13=73{displaystyle 2+{tfrac {1}{3}}={tfrac {7}{3}}} und nicht für 2⋅13=23{displaystyle 2cdot {tfrac {1}{3}}={tfrac {2}{3}}}.
Schreibt man dagegen abc{displaystyle a{tfrac {b}{c}}}, so handelt es sich nicht um einen Bruch in gemischter Schreibweise, sondern (wegen der Variablen) um einen Term. Hier muss das weggelassene Rechenzeichen ein Malpunkt sein (andere Rechenzeichen dürfen in Termen nicht weggelassen werden). abc{displaystyle a{tfrac {b}{c}}} muss also als a⋅bc{displaystyle acdot {tfrac {b}{c}}} verstanden werden und niemals als a+bc{displaystyle a+{tfrac {b}{c}}}.
Rechenregeln
Praktisches Rechnen mit Brüchen
Beim Rechnen mit Brüchen in den vier Grundrechenarten Addition, Subtraktion, Multiplikation und Division werden jeweils zwei Brüche verknüpft, sodass eine dritte Zahl entsteht. Dies darf nicht verwechselt werden mit dem Umformen von Brüchen, wobei ein einziger Bruch eine neue Form erhält, ohne dass sein Wert sich ändert.
Das Umformen (die Formänderung) ist oft die Voraussetzung dafür, dass mit Brüchen gerechnet werden kann. Deshalb wird es hier zuerst behandelt.
Formänderung von Brüchen
Umrechnen in eine Dezimalzahl
Um einen Bruch in eine Dezimalzahl umzuwandeln, dividiert man einfach den Zähler durch den Nenner. 34{displaystyle {tfrac {3}{4}}} ergibt 0,75 beziehungsweise 75 % vom Ganzen.
Erweitern und kürzen
Der Wert der durch einen Bruch dargestellten Bruchzahl ändert sich nicht, wenn man Zähler und Nenner des Bruches mit derselben Zahl (ungleich 0) multipliziert (den Bruch erweitert) oder durch einen gemeinsamen Teiler von Zähler und Nenner teilt (den Bruch kürzt).
Beispiel: 23=2⋅33⋅3=69{displaystyle {tfrac {2}{3}}={tfrac {2cdot 3}{3cdot 3}}={tfrac {6}{9}}}. Von links nach rechts gelesen wurde der Bruch erweitert, von rechts nach links gekürzt.
Gemischte Zahlen einrichten und Ganze abspalten
Der Wert einer in gemischter Schreibweise dargestellten Bruchzahl ändert sich nicht, wenn man den ganzzahligen Anteil als Scheinbruch mit dem Nenner des Bruchteils schreibt und die verbliebenen Bruchanteile hinzuzählt. Umgekehrt kann man bei einem unechten Bruch die Bruchteile, die Ganze ergeben, abspalten und die verbleibenden als Bruch anfügen.
Beispiel: 83=63+23=2+23=223{displaystyle {tfrac {8}{3}}={tfrac {6}{3}}+{tfrac {2}{3}}=2+{tfrac {2}{3}}=2{tfrac {2}{3}}}. Von links nach rechts gelesen wurden Ganze abgespalten, von rechts nach links wurde die gemischte Zahl eingerichtet.
Brüche gleichnamig machen
Gemeine Brüche, die in ihrem Nenner übereinstimmen, heißen gleichnamig. Werden Brüche so erweitert, dass sie danach die gleichen Nenner haben, so nennt man das gleichnamig machen. Beim praktischen Rechnen sollte dazu der Hauptnenner der Brüche bestimmt werden, das ist das kleinste gemeinsame Vielfache (kgV) der Nenner.
Beispiel: Die Brüche 27;16;914{displaystyle {tfrac {2}{7}};{tfrac {1}{6}};{tfrac {9}{14}}} sollen gleichnamig gemacht werden. Das kgV der Nenner ist 2⋅3⋅7=42{displaystyle 2cdot 3cdot 7=42}, also werden alle drei Brüche so erweitert, dass ihr Nenner 42 lautet:
27=2⋅642=1242;16=1⋅742=742;914=9⋅342=2742{displaystyle {tfrac {2}{7}}={tfrac {2cdot 6}{42}}={tfrac {12}{42}};quad {tfrac {1}{6}}={tfrac {1cdot 7}{42}}={tfrac {7}{42}};quad {tfrac {9}{14}}={tfrac {9cdot 3}{42}}={tfrac {27}{42}}}.
Die gleichnamigen Darstellungen lassen sich nun beispielsweise verwenden, um die dargestellten Bruchzahlen der Größe nach zu ordnen, indem man ihre Zähler vergleicht:
742<1242<2742{displaystyle {tfrac {7}{42}}<{tfrac {12}{42}}<{tfrac {27}{42}};;}, also muss 16<27<914{displaystyle ;;{tfrac {1}{6}}<{tfrac {2}{7}}<{tfrac {9}{14}};} gelten.
Die Grundrechenarten
Addieren und Subtrahieren

Beispiel einer Addition von zwei gleichnamigen gemeinen Brüchen.34+14=1{displaystyle {tfrac {3}{4}}+{tfrac {1}{4}}=1} Man liest: „drei Viertel plus ein Viertel“
Die Brüche, die addiert oder subtrahiert werden sollen, werden zunächst gleichnamig gemacht, anschließend werden ihre Zähler addiert bzw. subtrahiert.
Beispiel: 16+215=530+430=930=310{displaystyle {tfrac {1}{6}}+{tfrac {2}{15}}={tfrac {5}{30}}+{tfrac {4}{30}}={tfrac {9}{30}}={tfrac {3}{10}}}.
Multiplizieren
Brüche werden multipliziert, indem man ihre Zähler und Nenner miteinander multipliziert. Das Produkt der Zähler ist dann der Zähler des Ergebnisses, das Produkt der Nenner ist dann der Nenner des Ergebnisses.
Beispiel: 23⋅914=2⋅93⋅14=37{displaystyle {tfrac {2}{3}}cdot {tfrac {9}{14}}={tfrac {2cdot 9}{3cdot 14}}={tfrac {3}{7}}}.
Dividieren
Durch einen Bruch wird dividiert, indem man mit seinem Kehrwert multipliziert.
Beispiel: 215:1427=215⋅2714=23⋅5⋅3⋅92⋅7=1⋅95⋅7=935{displaystyle {tfrac {2}{15}}:{tfrac {14}{27}}={tfrac {2}{15}}cdot {tfrac {27}{14}}={tfrac {2}{3cdot 5}}cdot {tfrac {3cdot 9}{2cdot 7}}={tfrac {1cdot 9}{5cdot 7}}={tfrac {9}{35}}}.
Dabei dürfen, wie im Beispiel dargestellt, Zwischenergebnisse gekürzt werden (hier beispielsweise die 3 und die 2 im vorletzten Schritt).
Rechnen mit gemischten Brüchen
Beim Multiplizieren oder Dividieren von gemischten Brüchen ist es meist nötig, diese zunächst in gewöhnliche Brüche umzuwandeln. (Außer bei ganz einfachen Aufgaben, wie etwa 613:2=316{displaystyle 6{tfrac {1}{3}}:2=3{tfrac {1}{6}}}.)
Beim Addieren und Subtrahieren dagegen ist es viel günstiger, die Ganzen für sich zu betrachten und Bruchrechnung nur bei den verbleibenden echten Brüchen anzuwenden. Beim Addieren kann hier ein zusätzliches Ganzes auftreten, beim Subtrahieren mögen die Bruchteile nicht ausreichen, sodass eines der Ganzen zu einem Scheinbruch aufgeteilt werden muss:
1334+2712=40+(34+12)=40+114=4114{displaystyle 13{tfrac {3}{4}}+27{tfrac {1}{2}}=40+left({tfrac {3}{4}}+{tfrac {1}{2}}right)=40+1{tfrac {1}{4}}=41{tfrac {1}{4}}};
1613−912=7+(13−12)=7+(26−36)=6+(66+26−36)=656{displaystyle 16{tfrac {1}{3}}-9{tfrac {1}{2}}=7+left({tfrac {1}{3}}-{tfrac {1}{2}}right)=7+left({tfrac {2}{6}}-{tfrac {3}{6}}right)=6+left({tfrac {6}{6}}+{tfrac {2}{6}}-{tfrac {3}{6}}right)=6{tfrac {5}{6}}}.
Abstrakte Rechenregeln
Die folgenden Regeln gelten sowohl beim Bruchrechnen im engeren Sinn als auch beim Rechnen mit Bruchtermen.
Beim Rechnen mit Brüchen stehen die Variablen a,b,c,d,n{displaystyle a,;b,;c,;d,;n;} in den Regeln für bestimmte ganze Zahlen. Setzt man stattdessen für diese Variablen andere Ausdrücke, z. B. selbst wieder echte Brüche, Dezimalbrüche oder Terme ein, dann erhält man Regeln für das Rechnen mit Bruchtermen, das Bruchrechnen im weiteren Sinn.
Beim Rechnen mit Brüchen liefern die abstrakten Rechenregeln stets korrekte Ergebnisse, häufig ist die Rechnung mit den „praktischen Rechenregeln“ weniger aufwändig.
Erweitern und Kürzen
| Kürzen →{displaystyle rightarrow } |
|---|
a⋅cb⋅c=ab{displaystyle {frac {acdot c}{bcdot c}}={frac {a}{b}}} |
←{displaystyle leftarrow } Erweitern |
Hilfreiche Eselsbrücken hierzu sind:
- Faktoren kürzen, das ist brav; wer Summen kürzt, der ist ein Schaf.
- Differenzen und Summen kürzen nur die Dummen.
- Was du oben tust, machst du auch unten!
Aus der Äquivalenz ab=a⋅cb⋅c{displaystyle {frac {a}{b}}={frac {acdot c}{bcdot c}}} für beliebige natürliche Zahlen c>0{displaystyle c>0} folgt, dass jede rationale Zahl durch unendlich viele verschiedene Brüche dargestellt werden kann, denn es gilt ab=2a2b=3a3b=4a4b=⋯{displaystyle {frac {a}{b}}={frac {2a}{2b}}={frac {3a}{3b}}={frac {4a}{4b}}=dotsb }.
Addition
- ab+cd=a⋅d+c⋅bb⋅d{displaystyle {frac {a}{b}};+;{frac {c}{d}};=;{frac {acdot d+ccdot b}{bcdot d}}}
Subtraktion
- ab−cd=a⋅d−c⋅bb⋅d{displaystyle {frac {a}{b}}-{frac {c}{d}};=;{frac {acdot d-ccdot b}{bcdot d}}}
Multiplikation
- ab⋅cd=a⋅cb⋅d{displaystyle {frac {a}{b}};cdot ;{frac {c}{d}};=;{frac {acdot c}{bcdot d}}}
- ab⋅n=a⋅nb{displaystyle {frac {a}{b}};cdot ;n;=;{frac {acdot n}{b}}}
Division
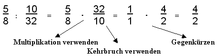
Beispiel für die Division durch einen Bruch
- ab:cd=ab⋅dc=a⋅db⋅c{displaystyle {frac {a}{b}}:{frac {c}{d}};=;{frac {a}{b}};cdot ;{frac {d}{c}};=;{frac {acdot d}{bcdot c}}}
Man dividiert also durch einen Bruch, indem man mit dem Kehrwert des Bruches, der als Divisor fungiert, multipliziert. Die Division wird also auf die Multiplikation zurückgeführt.
- ab:n=ab⋅nundn:ab=n⋅ba{displaystyle {frac {a}{b}}:n;=;{frac {a}{bcdot n}}quad {text{und}}quad n:{frac {a}{b}};=;{frac {ncdot b}{a}}}
Potenzen
| Regel | Beispiel |
|---|---|
anbm=an⋅b−m{displaystyle {frac {a^{n}}{b^{m}}}=a^{n}cdot b^{-m}} | 32=3⋅2−1{displaystyle {frac {3}{2}}=3cdot 2^{-1}} |
anam=an−m{displaystyle {frac {a^{n}}{a^{m}}}=a^{n-m}} | a3a2=a3⋅a−2=a3−2=a{displaystyle {frac {a^{3}}{a^{2}}}=a^{3}cdot a^{-2}=a^{3-2}=a} |
anbn=(ab)n{displaystyle {frac {a^{n}}{b^{n}}}=left({frac {a}{b}}right)^{n}} | 3222=(32)2{displaystyle {frac {3^{2}}{2^{2}}}=left({frac {3}{2}}right)^{2}} |
Rechnen mit Bruchtermen
Bruchterme, also Rechenausdrücke in der Form von gemeinen Brüchen, spielen in der elementaren Algebra eine wichtige Rolle. Im Allgemeinen enthalten Bruchterme neben Zahlen auch Variablen.
Die Rechenregeln für Brüche können auch auf Bruchterme angewendet werden.
Definitionsbereich
Bei der Bestimmung des Definitionsbereiches eines Bruchterms ist zu beachten, dass der Nenner nicht den Wert 0 haben darf. Beispielsweise wäre der von x{displaystyle x} abhängige Bruchterm 16−2x{displaystyle {tfrac {1}{6-2x}}} beim Einsetzen von x=3{displaystyle x=3} nicht definiert.
Der Definitionsbereich ist also D=R∖{3}{displaystyle D=mathbb {R} setminus {3}}, wenn als Grundmenge die Menge der reellen Zahlen vorausgesetzt wird.
In komplizierteren Fällen sollte der Nenner in Faktoren zerlegt werden, damit der Definitionsbereich erkennbar wird.
Beispiel: xx2−9=x(x+3)(x−3){displaystyle {tfrac {x}{x^{2}-9}}={tfrac {x}{(x+3)(x-3)}}} hat den Definitionsbereich D=R∖{−3;+3}{displaystyle D=mathbb {R} setminus {-3;+3}}.
Kürzen
Kürzen bedeutet, dass man Zähler und Nenner durch denselben Rechenausdruck dividiert.
Wichtig dabei ist, dass nur Faktoren von Produkten herausgekürzt werden können. Summen und Differenzen im Zähler und im Nenner müssen gegebenenfalls zuerst
in Produkte zerlegt werden (Faktorisierung).
Beispiele:
- 4abc36a2bc=2c23a{displaystyle quad {frac {4abc^{3}}{6a^{2}bc}}={frac {2c^{2}}{3a}}}
- x2−6xy+9y22x−6y=(x−3y)22(x−3y)=x−3y2{displaystyle quad {frac {x^{2}-6xy+9y^{2}}{2x-6y}}={frac {(x-3y)^{2}}{2(x-3y)}}={frac {x-3y}{2}}}
Beim Kürzen eines Bruchterms kann sich der Definitionsbereich ändern! So ist im ersten Beispiel der ungekürzte, links stehende Term nur definiert, wenn a,b,c≠0{displaystyle a,b,cneq 0} gilt, der rechtsstehende bereits, wenn nur a≠0{displaystyle aneq 0} gilt. Im zweiten Beispiel ist der ungekürzte Term nur definiert, wenn x≠3y{displaystyle xneq 3y} gilt, der gekürzte ist ohne Einschränkungen definiert.
Die Änderung des Definitionsbereiches eines Bruchterms beim Kürzen ist eine der Techniken, mit denen Funktionsterme stetig fortgesetzt werden können.
Addition und Subtraktion
Wie bei Zahlen ist es nötig, die gegebenen Bruchterme gleichnamig zu machen, d. h. auf den gleichen Nenner zu bringen. Man bestimmt einen möglichst einfachen gemeinsamen Nenner (Hauptnenner), der durch alle gegebenen Nenner teilbar ist.
Beispiel:
- 32a2−4ab−12ab+2{displaystyle {frac {3}{2a^{2}}}-{frac {4ab-1}{2ab}}+2}
Als Hauptnenner ergibt sich 2a2b{displaystyle 2a^{2}b}. Die Erweiterungsfaktoren der drei gegebenen Bruchterme erhält man dadurch, dass man jeweils den gefundenen Hauptnenner durch den bisherigen Nenner dividiert. Die Erweiterungsfaktoren sind also b{displaystyle b},
a{displaystyle a} und 2a2b{displaystyle 2a^{2}b}.
- 32a2−4ab−12ab+2{displaystyle {frac {3}{2a^{2}}}-{frac {4ab-1}{2ab}}+2}
- =3⋅b−(4ab−1)⋅a+2⋅2a2b2a2b{displaystyle ={frac {3cdot b-(4ab-1)cdot a+2cdot 2a^{2}b}{2a^{2}b}}}
- =3b−4a2b+a+4a2b2a2b=3b+a2a2b{displaystyle ={frac {3b-4a^{2}b+a+4a^{2}b}{2a^{2}b}}={frac {3b+a}{2a^{2}b}}}
Häufig lässt sich der Hauptnenner nur erkennen, wenn man die Nenner in Faktoren zerlegt (Faktorisierung). Dabei greift man oft auf die Methode des Ausklammerns zurück oder verwendet binomische Formeln.
Beispiel:
- xx2−xy−yx2+xy−xx2−y2{displaystyle {frac {x}{x^{2}-xy}}-{frac {y}{x^{2}+xy}}-{frac {x}{x^{2}-y^{2}}}}
- =xx(x−y)−yx(x+y)−x(x+y)(x−y){displaystyle ={frac {x}{x(x-y)}}-{frac {y}{x(x+y)}}-{frac {x}{(x+y)(x-y)}}}
- =x⋅(x+y)−y⋅(x−y)−x⋅xx(x+y)(x−y){displaystyle ={frac {xcdot (x+y)-ycdot (x-y)-xcdot x}{x(x+y)(x-y)}}}
- =x2+xy−xy+y2−x2x(x+y)(x−y)=y2x(x+y)(x−y){displaystyle ={frac {x^{2}+xy-xy+y^{2}-x^{2}}{x(x+y)(x-y)}}={frac {y^{2}}{x(x+y)(x-y)}}}
Multiplikation und Division
Beim Multiplizieren von Bruchtermen müssen sowohl die Zähler als auch die Nenner multipliziert werden. Gemeinsame Faktoren von Zähler und Nenner sollten herausgekürzt werden.
Beispiel: 4xyz2⋅xz6y=4x2yz6yz2=2x23z{displaystyle {frac {4xy}{z^{2}}}cdot {frac {xz}{6y}}={frac {4x^{2}yz}{6yz^{2}}}={frac {2x^{2}}{3z}}}
In komplizierteren Aufgaben sollte man Zähler und Nenner in Faktoren zerlegen, um sie bereits vor der eigentlichen Multiplikation herauskürzen zu können.
Beispiel: a−2b4a+1⋅16a2−1a2−4ab+4b2=a−2b4a+1⋅(4a+1)(4a−1)(a−2b)2=4a−1a−2b{displaystyle {frac {a-2b}{4a+1}}cdot {frac {16a^{2}-1}{a^{2}-4ab+4b^{2}}}={frac {a-2b}{4a+1}}cdot {frac {(4a+1)(4a-1)}{(a-2b)^{2}}}={frac {4a-1}{a-2b}}}
Die Division von Bruchtermen lässt sich auf die Multiplikation zurückführen. Man dividiert durch einen Bruchterm, indem man mit seinem Kehrwert multipliziert.
Beispiel: 2x−35x:4x2−910x2=2x−35x⋅10x2(2x+3)(2x−3)=2x2x+3{displaystyle {frac {2x-3}{5x}}:{frac {4x^{2}-9}{10x^{2}}}={frac {2x-3}{5x}}cdot {frac {10x^{2}}{(2x+3)(2x-3)}}={frac {2x}{2x+3}}}
Weitere Darstellungsformen
Partialbrüche
Brüche kann man oft in sogenannte Partialbrüche zerlegen, deren Nenner ganze Potenzen von Primzahlen sind; z. B.:
- 56=12+13,{displaystyle {frac {5}{6}}={frac {1}{2}}+{frac {1}{3}},}
- 16=12−13,{displaystyle {frac {1}{6}}={frac {1}{2}}-{frac {1}{3}},,}
- 172=18−19,{displaystyle {frac {1}{72}}={frac {1}{8}}-{frac {1}{9}},}
- 160=−14−43+85.{displaystyle {frac {1}{60}}={frac {-1}{4}}-{frac {4}{3}}+{frac {8}{5}}.}
Ägyptische Brüche
Es gibt auch Zerlegungen als sogenannte ägyptische Brüche (Stammbrüche), z. B.
37=13+111+1231{displaystyle {frac {3}{7}}={frac {1}{3}}+{frac {1}{11}}+{frac {1}{231}}} und
2531=12+14+118+11116{displaystyle {frac {25}{31}}={frac {1}{2}}+{frac {1}{4}}+{frac {1}{18}}+{frac {1}{1116}}},
die alten Ägypter kannten nur solche Summen und haben mit diesen gerechnet.
Pythagoreische Brüche
Das Zahlentripel (15,2435,57){displaystyle ({tfrac {1}{5}},{tfrac {24}{35}},{tfrac {5}{7}})} ist ein Beispiel eines pythagoreischen Bruchs (siehe auch pythagoreisches Tripel), denn
(15)2+(2435)2=(57)2{displaystyle left({frac {1}{5}}right)^{2}+left({frac {24}{35}}right)^{2}=left({frac {5}{7}}right)^{2}}.
Rationaler Zähler oder Nenner
Siehe Rationalisierung (Bruchrechnung).
Verallgemeinerungen
Die Konstruktion des Körpers der rationalen Zahlen als Brüche aus dem Ring der ganzen Zahlen wird in der abstrakten Algebra durch das Konzept des Quotientenkörpers auf beliebige Integritätsringe verallgemeinert.
Siehe auch
- Farey-Folge
- Kreuzweise Multiplikation
Literatur
- Erhard Cramer, Johanna Nešlehová: Vorkurs Mathematik. Arbeitsbuch zum Studienbeginn in Bachelor-Studiengängen. 3., verb. Auflage. Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-78180-6, S. 77–83 ((eingeschränkte Online-Kopie in der Google-Buchsuche-USA)).
- Friedhelm Padberg: Gemeine Brüche – Dezimalbrüche. Didaktik der Bruchrechnung. BI-Wissenschafts-Verlag, 1989, ISBN 3-411-03207-3.
Weblinks
Bruchrechnung In Nachhilfe Videos veranschaulicht (Olaf Hinrichsen, OberPrima.com UG, 16. März 2018)
Rechner für Brüche – diverse Online-Programme rund um die Bruchrechnung
Formeln für die Bruchrechnung – Eine übersichtliche Auflistung der wichtigsten Formeln für das Rechnen mit Brüchen- Interaktives Applet, das durch die verschiedene Aufgabenstellungen zur Bruchrechnung führt
Einzelnachweise
↑ Amtliche Rechtschreibregeln vom 1. August 2006, §106, canoo.net






























































































