Vryjdfkk

Der Kosinussatz ist ein elementarer Lehrsatz der Trigonometrie, eines der Teilgebiete der Mathematik. Er beinhaltet drei Identitätsgleichungen, welche die Beziehungen zwischen den Längen der Seiten von Dreiecken und den Kosinuswerten ihrer Winkel darstellen.

Formulierung |

Allgemeine Formulierung |

Bezeichnungen im Dreieck

Für die drei Seiten a{displaystyle a}, b{displaystyle b} und c{displaystyle c} eines Dreiecks sowie für den der Seite c{displaystyle c} gegenüberliegenden Winkel (d. h. den zwischen den Seiten a{displaystyle a} und b{displaystyle b} liegenden Winkel) γ{displaystyle gamma } gilt:

c2=a2+b2−2abcos⁡γ{displaystyle c^{2}=a^{2}+b^{2}-2,a,b,cos gamma }

Umkehrung für den Winkel:

cos⁡γ=a2+b2−c22ab{displaystyle cos gamma ={frac {a^{2}+b^{2}-c^{2}}{2,a,b}}}

Entsprechend gilt für die anderen Winkel:

b2=a2+c2−2accos⁡β{displaystyle b^{2}=a^{2}+c^{2}-2,a,c,cos beta }

a2=b2+c2−2bccos⁡α{displaystyle a^{2}=b^{2}+c^{2}-2,b,c,cos alpha }^[1]

Gleichwertige Formulierung |

Die zuvor genannten drei Identitätsgleichungen sind ihrerseits Folgerungen aus (und im Rahmen der Trigonometrie der euklidischen Ebene sogar gleichwertig mit) den folgenden drei Kosinusformeln:^[2][3]

a=bcos⁡γ+ccos⁡β{displaystyle a=bcos {gamma }+ccos {beta }}

b=ccos⁡α+acos⁡γ{displaystyle b=ccos {alpha }+acos {gamma }}

c=acos⁡β+bcos⁡α{displaystyle c=acos {beta }+bcos {alpha }}

Man fasst diese Formeln unter dem Stichwort Projektionssatz^[4] oder Projektionssätze^[2] zusammen.^[5]

Der Satz des Pythagoras als Spezialfall des Kosinussatzes |

Mit γ=90∘=π2{displaystyle textstyle gamma =90^{circ }={frac {pi }{2}}}, also bei einem rechtwinkligen Dreieck, gilt cos⁡γ=cos⁡π2=0{displaystyle textstyle cos gamma =cos {frac {pi }{2}}=0}. Dadurch ergibt sich als Spezialfall des Kosinussatzes im rechtwinkligen Dreieck der Satz des Pythagoras:

c2=a2+b2.{displaystyle c^{2}=a^{2}+b^{2}.}

Der Kosinussatz stellt daher eine Verallgemeinerung des Satzes von Pythagoras dar und wird auch erweiterter Satz des Pythagoras genannt.

Anwendungen |

Zahlenbeispiel |

In einem Dreieck ABC sind folgende Seitengrößen bekannt (Bezeichnungen wie üblich):

a=4,00cm{displaystyle a=4{,}00;{rm {cm}}}

b=2,00cm{displaystyle b=2{,}00;{rm {cm}}}

c=3,70cm{displaystyle c=3{,}70;{rm {cm}}}

Gesucht ist die Winkelgröße β{displaystyle beta } (Bezeichnungen wie üblich).

b2=a2+c2−2⋅a⋅c⋅cos⁡β{displaystyle b^{2}=a^{2}+c^{2}-2cdot acdot ccdot cos beta }

2⋅a⋅c⋅cos⁡β=a2+c2−b2{displaystyle 2cdot acdot ccdot cos beta =a^{2}+c^{2}-b^{2}}

cos⁡β=a2+c2−b22⋅a⋅c=(4,0cm)2+(3,7cm)2−(2,0cm)22⋅4,0cm⋅3,7cm=0,868{displaystyle cos beta ,=,{frac {a^{2}+c^{2}-b^{2}}{2cdot acdot c}}={frac {(4{,}0,{rm {cm}})^{2}+(3{,}7,{rm {cm}})^{2}-(2{,}0,{rm {cm}})^{2}}{2cdot 4{,}0,{rm {cm}}cdot 3{,}7,{rm {cm}}}}=0{,}868}

β=29,8∘{displaystyle beta =29,8^{circ }}

Kongruenzsätze |

Die Kongruenzsätze SSS (Seite-Seite-Seite) und SWS (Seite-Winkel-Seite) besagen, dass ein Dreieck durch die Vorgabe von drei Seiten oder von zwei Seiten und ihrem Zwischenwinkel vollständig bestimmt ist. Alternativ kann man auch jeweils zwei Vektoren angeben, aus denen der eingeschlossene Winkel berechnet werden kann. Der Kosinussatz erlaubt es in diesen Fällen, aus den drei gegebenen Stücken ein viertes Stück, nämlich einen Winkel (im Fall SSS) beziehungsweise die dritte Seite (im Fall SWS) zu berechnen. Wenn man anschließend auch die übrigen Winkel eines Dreiecks ermitteln möchte, kann man wahlweise nochmal den Kosinussatz (mit auf den gesuchten Winkel angepassten Seitenbezeichnungen) oder den Sinussatz anwenden. Den letzten Winkel berechnet man am zweckmäßigsten über die Winkelsumme von 180°.

Wenn nur eine Seite und zwei Winkel gegeben sind (Kongruenzsätze SWW oder WSW) oder zwei Seiten und der Gegenwinkel der größeren Seite (Kongruenzsatz SsW), so berechnet man zunächst eines der fehlenden Stücke mit dem Sinussatz und den fehlenden Winkel über die Winkelsumme, bevor man mit dem Kosinussatz die dritte Seite bestimmen kann.

Verallgemeinerung |

Mit Vektoren in reellen Skalarprodukträumen, also Vektorräumen V{displaystyle V} mit Skalarprodukt ⟨⋅,⋅⟩{displaystyle langle cdot ,cdot rangle }, kann auch der Kosinussatz leicht verallgemeinert werden. Bezeichnet

‖a‖=⟨a,a⟩{displaystyle |a|={sqrt {langle a,arangle }}}

die Skalarproduktnorm, also die Länge, eines Vektors a∈V{displaystyle ain V} und θa,b{displaystyle theta _{a,b}} mit

cos⁡θa,b=⟨a,b⟩‖a‖‖b‖{displaystyle cos theta _{a,b}={frac {langle a,brangle }{|a|,|b|}}}

den Winkel zwischen den beiden Vektoren a,b∈V{displaystyle a,bin V}, dann gilt für die Norm des Vektors c=b−a{displaystyle c=b-a}:

‖c‖2=‖b−a‖2=⟨b−a,b−a⟩=⟨b,b⟩−⟨b,a⟩−⟨a,b⟩+⟨a,a⟩==‖a‖2+‖b‖2−2⟨a,b⟩=‖a‖2+‖b‖2−2‖a‖‖b‖cos⁡θa,b.{displaystyle {begin{aligned}|c|^{2}&=|b-a|^{2}=langle b-a,b-arangle =langle b,brangle -langle b,arangle -langle a,brangle +langle a,arangle =\&=|a|^{2}+|b|^{2}-2langle a,brangle =|a|^{2}+|b|^{2}-2|a|,|b|cos theta _{a,b}.end{aligned}}}

Beweis |

Elementargeometrischer Beweis |

Im folgenden Beweis wird γ<90∘{displaystyle gamma <90^{circ }} vorausgesetzt. Für γ>90∘{displaystyle gamma >90^{circ }} muss der Beweis geringfügig modifiziert werden. Für γ=90∘{displaystyle gamma =90^{circ }} ergibt sich der Kosinussatz direkt aus dem Satz des Pythagoras.

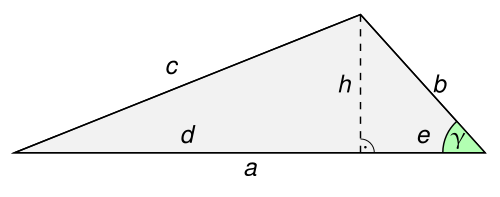
In den Teildreiecken soll der Satz des Pythagoras angewandt werden, um einen Rechenausdruck für c2{displaystyle c^{2}} zu finden. Dazu benötigt man die Quadrate der Kathetenlängen dieses Teildreiecks:

h2=b2−e2{displaystyle h^{2},=b^{2}-e^{2}} (Satz des Pythagoras für das rechte Teildreieck)

d2=(a−e)2=a2−2⋅a⋅e+e2{displaystyle d^{2}=(a-e)^{2}=a^{2}-2cdot acdot e+e^{2}} (binomische Formel)

Nach Pythagoras gilt für das linke Teildreieck:

c2=h2+d2{displaystyle c^{2},=h^{2}+d^{2}}

Es müssen also die beiden oben gefundenen Rechenausdrücke addiert werden:

c2=b2−e2+a2−2⋅a⋅e+e2=a2+b2−2⋅a⋅e{displaystyle c^{2}=b^{2}-e^{2}+a^{2}-2cdot acdot e+e^{2}=a^{2}+b^{2}-2cdot acdot e}

Zusätzlich gilt

cos⁡γ=eb{displaystyle cos gamma ={frac {e}{b}}} (=AnkatheteHypotenuse){displaystyle left(={frac {rm {Ankathete}}{rm {Hypotenuse}}}right)}

mit der Folgerung

e=b⋅cos⁡γ{displaystyle e=bcdot cos gamma }.

Einsetzen dieses Zwischenergebnisses in die Gleichung für c2{displaystyle c^{2}} ergibt die Behauptung:

c2=a2+b2−2⋅a⋅b⋅cos⁡γ{displaystyle c^{2}=a^{2}+b^{2}-2cdot acdot bcdot cos gamma }

Beweis mittels Vektorrechnung |

Anschließend an die Darstellung von Gericke und Raith wird zunächst der Beweis der drei Kosinusformeln (s. Projektionssatz im Abschnitt „Gleichwertige Formulierung“) geführt:^[2][6]

Dazu macht man die Festlegungen

a→=BC→,b→=CA→,c→=AB→{displaystyle {vec {a}}={overrightarrow {BC}};,;{vec {b}}={overrightarrow {CA}};,;{vec {c}}={overrightarrow {AB}}}  .

Man erhält daraus die Gleichungen

−a→=CB→,−b→=AC→,−c→=BA→{displaystyle -{vec {a}}={overrightarrow {CB}};,;-{vec {b}}={overrightarrow {AC}};,;-{vec {c}}={overrightarrow {BA}}}

sowie unter Benutzung der Eigenschaften des Skalarprodukts

a=|a→|=|−a→|,b=|b→|=|−b→|,c=|c→|=|−c→|{displaystyle a=|{vec {a}}|=|-{vec {a}}|;,;b=|{vec {b}}|=|-{vec {b}}|;,;c=|{vec {c}}|=|-{vec {c}}|}

und

cos⁡α=⟨−b→,c→⟩|−b→|⋅|c→|=⟨−b→,c→⟩bc,cos⁡β=⟨−c→,a→⟩|−c→|⋅|a→|=⟨−c→,a→⟩ca,cos⁡γ=⟨−a→,b→⟩|−a→|⋅|b→|=⟨−a→,b→⟩ab{displaystyle cos {alpha }={frac {langle -{vec {b}},{vec {c}}rangle }{|-{vec {b}}|cdot |{vec {c}}|}}={frac {langle -{vec {b}},{vec {c}}rangle }{bc}};,;cos {beta }={frac {langle -{vec {c}},{vec {a}}rangle }{|-{vec {c}}|cdot |{vec {a}}|}}={frac {langle -{vec {c}},{vec {a}}rangle }{ca}};,;cos {gamma }={frac {langle -{vec {a}},{vec {b}}rangle }{|-{vec {a}}|cdot |{vec {b}}|}}={frac {langle -{vec {a}},{vec {b}}rangle }{ab}}}   .^[7]

Nun zieht man die für das Dreieck charakteristische Grundgleichung

a→+b→+c→=0→{displaystyle {vec {a}}+{vec {b}}+{vec {c}}={vec {0}}}

heran und gewinnt

a→=(−b→)+(−c→){displaystyle {vec {a}}=(-{vec {b}})+(-{vec {c}})}

und weiter

a2=|a→|2=⟨a→,a→⟩=⟨−b→,a→⟩+⟨−c→,a→⟩{displaystyle a^{2}=|{vec {a}}|^{2}=langle {vec {a}},{vec {a}}rangle =langle -{vec {b}},{vec {a}}rangle +langle -{vec {c}},{vec {a}}rangle }   .

Folglich ergibt sich

a=⟨−b→,a→⟩a+⟨−c→,a→⟩a=⟨−a→,b→⟩a+⟨−c→,a→⟩a=bcos⁡γ+ccos⁡β{displaystyle a={frac {langle -{vec {b}},{vec {a}}rangle }{a}}+{frac {langle -{vec {c}},{vec {a}}rangle }{a}}={frac {langle -{vec {a}},{vec {b}}rangle }{a}}+{frac {langle -{vec {c}},{vec {a}}rangle }{a}}=bcos {gamma }+ccos {beta }}

und damit die erste der obigen drei Kosinusformeln.

Die beiden anderen erhält man auf gleiche Art und Weise.

Auf die drei Formeln der allgemeinen Formulierung kann man dann mittels elementarer algebraischer Operationen schließen. So erhält man (etwa) die erste Gleichung, indem die in den zuvor stehenden drei Kosinusformeln nacheinander mit a,b,(−c){displaystyle a;,;b;,;(-c)} multipliziert, aufaddiert und nach c2{displaystyle c^{2}} auflöst.

Siehe auch |

• Sinussatz


• Tangenssatz


• Geometrie auf der Kugeloberfläche


• Dschamschid Masʿud al-Kaschi

Quellen und Literatur |

• 
  Ilka Agricola, Thomas Friedrich: Elementargeometrie. Fachwissen für Studium und Mathematikunterricht (= Studium). 4., überarbeitete Auflage. Springer Spektrum, Wiesbaden 2015, ISBN 978-3-658-06730-4, doi:10.1007/978-3-658-06731-1. 
  


• 
  Heinrich Behnke, Friedrich Bachmann, Kuno Fladt, Wilhelm Süss (Hrsg.): Grundzüge der Mathematik. Band II. Geometrie. Vandenhoeck & Ruprecht, Göttingen 1960. 
  


• 
  I. N. Bronstein, K. A. Semendjajev, G. Musiol, H. Mühlig (Hrsg.): Taschenbuch der Mathematik. 7., vollständig überarbeitete und ergänzte Auflage. Verlag Harri Deutsch, Frankfurt am Main 2008, ISBN 978-3-8171-2007-9. 
  


• 
  Hanfried Lenz: Grundlagen der Elementarmathematik. 3., überarbeitete Auflage. Hanser Verlag, München (u. a.) 1976, ISBN 3-446-12160-9. 
  


• Manfred Leppig (Hrsg.): Lernstufen Mathematik. 1. Auflage. Girardet, Essen 1981, ISBN 3-7736-2005-5, S. 192–193. 
  

Weblinks |

 Commons: Law of cosines – Sammlung von Bildern, Videos und Audiodateien

• 
  Kosinussatz – Illustration und Beweis auf www.arndt-bruenner.de


• Herleitung des Kosinussatzes sowie Anwendung (Video)


• 
  Law of Cosines – 2 Beweise auf proofwiki.org (engl.)

Einzelnachweise und Fußnoten |

1. 
   ↑ Beweis siehe auch: Wikibooks-Beweisarchiv
   


2. 
   ↑ ^abc Helmuth Gericke, F. Raith: Vektoren und Trigonometrie. in: H. Behnke et al.: Grundzüge der Mathematik. Band II. Geometrie., 1960, S. 266 ff
   


3. 
   ↑ Hanfried Lenz: Grundlagen der Elementarmathematik., 1976, S. 236
   


4. 
   ↑ I. N. Bronstein, K. A. Semendjajev et al.: Taschenbuch der Mathematik. 2008, S. 146
   


5. 
   ↑ Als Folgerung aus dem Projektionssatz ergibt sich noch eine weitere interessante Kosinusformel; siehe Beweisarchiv.
   


6. 
   ↑ Der Beweis des Projektionssatzes lässt sich auch, und zwar in ähnlicher Weise wie der vorangehende Beweis, im Rahmen der Elementargeometrie führen.
   


7. 
   ↑ Es soll o.B.d.A. vorausgesetzt sein, dass ein nicht-ausgeartetes Dreieck vorliegt, also keine der drei Seiten und damit auch keiner der drei Vektoren die Länge 0{displaystyle 0} hat.