Vryjdfkk

Das Lebesgue-Maß  [.mw-parser-output .IPA a{text-decoration:none}ləˈbɛg] (nach Henri Léon Lebesgue) ist das Maß im euklidischen Raum, das geometrischen Objekten ihren Inhalt (Länge, Flächeninhalt, Volumen, …) zuordnet. Es ist ein Spezialfall des Lebesgue-Stieltjes-Maßes^[1] und dient zur Konstruktion des Lebesgue-Integrals.

Hintergrund |

Das Lebesgue-Maß ist aus der Sicht der modernen Mathematik der natürliche Begriff für Flächeninhalt und Volumen. Dieses Konzept ist das Endprodukt einer ganzen Reihe von Ideen, die versuchten, Begriffe wie Flächeninhalt und Volumen mathematisch exakt zu fassen. Erst mit dem Lebesgue-Maß kann dieser Prozess als abgeschlossen gelten. Das Lebesgue-Maß ordnet nicht nur einfachen geometrischen Objekten, sondern auch viel allgemeineren Mengen einschließlich aller offenen und abgeschlossenen Mengen einen Inhalt zu. Die Existenz einer nicht Lebesgue-messbaren Menge (etwa der Vitali-Mengen) lässt sich nicht-konstruktiv unter Verwendung des Auswahlaxioms beweisen. Es existieren verschiedene Sätze, dass eine solche Nicht-Konstruktivität in einem bestimmten Sinn notwendig ist, und dies unter bestimmten Annahmen sogar auf eine stärkere Weise als bei vielen anderen grundlegenden Sätzen der Analysis.

Definition |

Das Lebesgue-Borel-Maß auf der Borel-σ-Algebra B(Rn){displaystyle {mathcal {B}}(mathbb {R} ^{n})} (auch als Borel-Lebesgue-Maß oder nur Borel-Maß bezeichnet) ist das eindeutige Maß λ{displaystyle lambda } mit der Eigenschaft, dass es n{displaystyle n}-dimensionalen Hyperrechtecken ihr n{displaystyle n}-dimensionales Volumen zuordnet:

λ([a1,b1]×⋯×[an,bn])=(b1−a1)⋅…⋅(bn−an){displaystyle lambda ([a_{1},b_{1}]times dotsb times [a_{n},b_{n}])=(b_{1}-a_{1})cdot ldots cdot (b_{n}-a_{n})}.

Das heißt, es ist das Maß, das Intervallen ihre Länge zuordnet (im Eindimensionalen), Rechtecken ihren Flächeninhalt zuordnet (im Zweidimensionalen), Quadern ihr Volumen zuordnet (im Dreidimensionalen) usw. Durch diese Bedingung wird der Inhalt λ(B){displaystyle lambda (B)} beliebiger Borel-Mengen eindeutig festgelegt. Die Borel-Mengen werden auch Borel-messbar oder B-messbar genannt. Das Borel-Maß ist bewegungsinvariant und normiert, aber nicht vollständig.
Die Existenz des Lebesgue-Borel-Maßes wurde im Eindimensionalen zum ersten Mal von Émile Borel 1895 bewiesen, eine modernere Konstruktion über den Maßerweiterungssatz geht auf Constantin Carathéodory (1918) zurück.^[2]

Das Lebesgue-Maß ist das vollständige Maß λ{displaystyle lambda }, das man aus diesem Maß erhält, wenn man zu B(Rn){displaystyle {mathcal {B}}(mathbb {R} ^{n})} alle Mengen A{displaystyle A} hinzufügt, die zwischen zwei Borel-Mengen liegen (B1⊂A⊂B2{displaystyle B_{1}subset Asubset B_{2}}), welche denselben Inhalt haben, genauer λ(B2∖B1)=0{displaystyle lambda (B_{2}setminus B_{1})=0}, und so λ(A){displaystyle lambda (A)} festlegen. Die Mengen, für die das Lebesgue-Maß auf diese Weise definiert ist, heißen Lebesgue-messbar (oder L-messbar) und bilden die Lebesgue-σ{displaystyle sigma }-Algebra.

B-messbar und L-messbar |

Es lässt sich zeigen, dass die Menge der L-messbaren Mengen L(Rn){displaystyle {mathcal {L}}(mathbb {R} ^{n})} wesentlich größer als die Menge der B-messbaren Mengen ist:^[3][4]

card⁡(L(Rn))=card⁡(Pot⁡(Rn))=2card⁡(Rn)=2card⁡(R)>card⁡(R)=card⁡(Rn)=card⁡(B(Rn)),{displaystyle operatorname {card} ({mathcal {L}}(mathbb {R} ^{n}))=operatorname {card} (operatorname {Pot} (mathbb {R} ^{n}))=2^{operatorname {card} (mathbb {R} ^{n})}=2^{operatorname {card} (mathbb {R} )}>operatorname {card} (mathbb {R} )=operatorname {card} (mathbb {R} ^{n})=operatorname {card} ({mathcal {B}}(mathbb {R} ^{n})),,}

wobei card{displaystyle operatorname {card} } für Kardinalität und Pot{displaystyle operatorname {Pot} } für die Potenzmenge einer Menge steht.

Nullmengen |

Mengen, deren Lebesgue-Maß gleich 0 ist, werden Lebesgue-Nullmengen genannt. Abzählbare Mengen wie z. B. die Menge der rationalen Zahlen sind Lebesgue-Nullmengen. Ein Beispiel für eine überabzählbare Lebesgue-Nullmenge ist das Cantorsche Diskontinuum.^[5] Gilt eine mathematische Aussage für ein Gebiet mit Ausnahme einer Lebesgue-Nullmenge innerhalb des Gebietes, so sagt man: Die Aussage gilt Lebesgue-fast überall.

Eigenschaften |

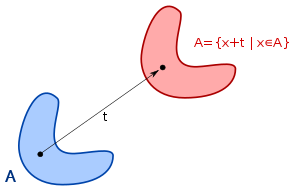
Da das Lebesgue-Maß translationsinvariant ist, ist das Lebesgue-Maß von A{displaystyle A} und A+t{displaystyle A+t} das gleiche.

Das Lebesgue-Maß ist das Haar-Maß auf der lokalkompakten topologischen Gruppe Rn{displaystyle mathbb {R} ^{n}} mit der Addition, die Existenz folgt daher bereits aus der Existenz des Haarmaßes. Insbesondere ist es translationsinvariant, das bedeutet, dass sich das Maß einer Menge unter Translation nicht ändert. Zudem ist es invariant unter Spiegelungen und Drehungen, also sogar bewegungsinvariant. Das Lebesgue-Maß ist σ-endlich und regulär.

Charakterisierung der Lebesgue-Messbarkeit |

Eine Teilmenge A{displaystyle A} des Rn{displaystyle mathbb {R} ^{n}} ist Lebesgue-messbar genau dann, wenn sie die folgende charakteristische Eigenschaft aufweist:^[6]

Zu jeder vorgegebenen Schranke ε>0{displaystyle varepsilon >0} gibt es im Rn{displaystyle mathbb {R} ^{n}} stets eine offene Menge U{displaystyle U} sowie eine abgeschlossene Menge F{displaystyle F} mit

F⊆A⊆U{displaystyle Fsubseteq Asubseteq U} und λn(U∖F)<ε{displaystyle lambda ^{n}(Usetminus F)<varepsilon }.

Konstruktion des Lebesgue-Maßes |

Eine mögliche Definition des Lebesgue-Maßes ist die Konstruktion von Carathéodory. Sei D{displaystyle {mathcal {D}}} die Menge der dyadischen Elementarzellen und vol⁡(Ai){displaystyle operatorname {vol} (A_{i})} das Volumen von Ai{displaystyle A_{i}}, da diese Mengen nur aus Produkten von Intervallen bestehen, definiert man das Volumen einfach als Produkt der einzelnen Seitenlängen. D{displaystyle {mathcal {D}}} ist ein Halbring und vol{displaystyle operatorname {vol} } ein σ{displaystyle sigma }-endlicher Inhalt, also ein Prämaß. Dieses Prämaß wird auch das Lebesguesche Prämaß genannt. Nach dem Maßerweiterungssatz von Carathéodory lässt es sich eindeutig zu einem Maß auf der erzeugten σ{displaystyle sigma }-Algebra, das sind gerade die Borel-Mengen, fortsetzen. Diese Fortsetzung ist das Lebesgue-Borel-Maß.

Konkret lässt sich der Beweis wie folgt führen (der Beweis des allgemeinen Maßerweiterungssatzes geht in den wesentlichen Punkten analog): Für eine gegebene Menge A⊆Rn{displaystyle Asubseteq mathbb {R} ^{n}} definiert man

λ∗(A):=inf{∑i≥1vol⁡(Ai):A⊆⋃i≥1Ai, Ai∈D}{displaystyle lambda ^{*}(A):=inf left{sum _{igeq 1}operatorname {vol} (A_{i}):Asubseteq bigcup _{igeq 1}A_{i}, A_{i}in {mathcal {D}}right}}.

Die Funktion λ∗{displaystyle lambda ^{*}} ist auf der gesamten Potenzmenge P(Rn){displaystyle {mathcal {P}}(mathbb {R} ^{n})} definiert und ein metrisches äußeres Maß, jedoch kein Maß. Um zu einem Maß zu kommen, kann man wie folgt von der Potenzmenge zu einem kleineren Mengensystem übergehen.

Eine Menge A∈P(Rn){displaystyle Ain {mathcal {P}}(mathbb {R} ^{n})} ist λ∗{displaystyle lambda ^{*}}-messbar, wenn für alle B∈P(Rn){displaystyle Bin {mathcal {P}}(mathbb {R} ^{n})} gilt:

λ∗(B)=λ∗(A∩B)+λ∗(B∖A){displaystyle lambda ^{*}(B)=lambda ^{*}(Acap B)+lambda ^{*}(Bsetminus A)}

(siehe Messbarkeit nach Carathéodory).

Alle bezüglich λ∗{displaystyle lambda ^{*}} messbaren Mengen aus P(Rn){displaystyle {mathcal {P}}(mathbb {R} ^{n})} bilden eine σ-Algebra A{displaystyle {mathcal {A}}} und λ∗{displaystyle lambda ^{*}} darauf ein Maß, d. h., λ:=λ∗|A{displaystyle lambda :=lambda ^{*}vert _{mathcal {A}}} ist ein Maß.

Siehe auch |

• Lebesgue-Integral


• 
  L^p-Raum

Quellen und weiterführende Informationen |

1. 
   ↑ Norbert Kusolitsch: Maß- und Wahrscheinlichkeitstheorie. Eine Einführung. 2., überarbeitete und erweiterte Auflage. Springer-Verlag, Berlin Heidelberg 2014, ISBN 978-3-642-45386-1, S. 68, doi:10.1007/978-3-642-45387-8. 
   


2. 
   ↑ Olav Kallenberg: Foundations of Modern Probability. 2nd edition. Springer, New York NY u. a. 2002, ISBN 0-387-95313-2, S. 570.
   


3. 
   ↑ Michael Leinert: Integration und Maß. Vieweg, Braunschweig u. a. 1995, ISBN 3-528-06385-8, 4.20.
   


4. 
   ↑ Beispiele für nicht B-messbare L-messbare Mengen sind zum ersten Mal von Suslin gegeben worden. Er hat dabei das System der sogenannten analytischen Mengen entwickelt, das eine echte Erweiterung des Systems der Borelschen Mengen ist und komplett im System der L-messbaren Mengen liegt.
   


5. 
   ↑ Das cantorsche Diskontinuum ist auch eine borelsche Nullmenge. Da das Lebesgue-Maß vollständig ist, sind alle Untermengen des cantorschen Diskontinuums L-messbar. Daraus folgt die erste von den oben erwähnten Ungleichungen – nämlich, dass das System der L-messbaren Mengen echt mächtiger als das Kontinuum ist.
   


6. 
   ↑ Jürgen Elstrodt: Maß- und Integrationstheorie., 7., korrigierte und aktualisierte, Springer, Heidelberg u. a. 2011, ISBN 978-3-642-17904-4, S. 67.