Vryjdfkk

Als Schwingungen oder Oszillationen (lateinisch oscillare ‚schaukeln‘) werden wiederholte zeitliche Schwankungen von Zustandsgrößen eines Systems bezeichnet.^[1][2] Unter Schwankung ist dabei die Abweichung von einem Mittelwert zu verstehen. Schwingungen können in allen rückgekoppelten Systemen auftreten.^[3] Beispiele für Schwingungen sind in der Mechanik, in der Elektrotechnik, der Biologie, in der Wirtschaft (Schweinezyklus) und in vielen anderen Bereichen anzutreffen.

Man unterscheidet:

• 
  periodische^[4] und nichtperiodische (quasiperiodische oder chaotische^[5][6]) Schwingungen


• ungedämpfte, gedämpfte und aperiodische Schwingungen


• freie, erzwungene (fremderregte), selbsterregte und parametererregte Schwingungen


• 
  lineare und nichtlineare Schwingungen


• Schwingungen mit einem Freiheitsgrad, mit mehreren Freiheitsgraden und mit unendlich vielen Freiheitsgraden (Schwingungen eines Kontinuums)


• kontinuierliche Schwingungen und Oszillation zwischen diskreten Zuständen

Alle diese Eigenschaften können kombiniert sein.

Als Vibration werden periodische, mit Verformung verbundene mechanische Schwingungen eines Körpers bezeichnet. Eine Schwingung, die zur Informationsübermittlung dient, nennt man manchmal Signal, zum Beispiel elektrisches Signal. Die räumliche Ausbreitung einer Störung oder Schwingung ist eine Welle.

Gegenüberstellung elementarer Schwingungsformen. Die waagerechte Achse stellt die Zeit dar

Harmonische Schwingungen |

Darstellung einer harmonischen Schwingung.

Als harmonisch wird eine Schwingung bezeichnet, deren Verlauf durch eine Sinusfunktion beschrieben werden kann.

Die Grafik zeigt eine harmonische Schwingung mit der Auslenkung y(t){displaystyle y(t)}, der Amplitude y0{displaystyle y_{0}} und der Periodendauer T{displaystyle T}.

Die Auslenkung y(t){displaystyle y(t)} zu einem Zeitpunkt t{displaystyle t} gibt den momentanen, die Amplitude den maximal möglichen Wert der Größe y{displaystyle y} an. Die Periodendauer oder die Schwingungsdauer ist die Zeit, die verstreicht, während ein schwingungsfähiges System genau eine Schwingungsperiode durchläuft, d. h. nach der es sich wieder im selben Schwingungszustand befindet. Der Kehrwert der Periodendauer T ist die Frequenz f, also: f=1T{displaystyle f={1 over T}quad }.
Statt f wird auch der griechische Buchstabe ν{displaystyle nu } (sprich: "nü") verwendet. Die Einheit der Frequenz ist Hertz (1 Hz = 1 s⁻¹).

Eine ungedämpfte Schwingung ist harmonisch, wenn die Rückstellgröße (die rückstellende Kraft) proportional zur Auslenkung beispielsweise eines Federpendels ist. Hierbei spricht man auch von einem harmonischen Oszillator oder einem linearen System, da die rückstellende Kraft sich linear mit der Auslenkung ändert: Verdoppelt sich diese, verdoppelt sich auch die rückstellende Kraft.

Eine solche Schwingung lässt sich beschreiben durch

y(t)=y0⋅sin⁡(2πft+φ0){displaystyle y(t)=y_{0}cdot sin(2pi ft+varphi _{0}),}

mit

y0{displaystyle y_{0}}  = Amplitude und

φ0{displaystyle varphi _{0}}  = Nullphasenwinkel der Schwingung.

Das 2π{displaystyle 2pi }-fache der Frequenz, ω=2π⋅f{displaystyle omega =2pi cdot f}, ist die Kreisfrequenz der Schwingung.
Durch Verwendung der Kreisfrequenz ergibt sich eine kompaktere Schreibweise:

y(t)=y0⋅sin⁡(ωt+φ0){displaystyle y(t)=y_{0}cdot sin(omega ,t+varphi _{0}),}

Linear gedämpfte Schwingung |

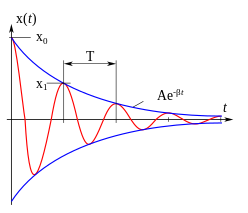Darstellung des zeitlichen Verlaufs der Größe x(t){displaystyle x(t)} bei einer freien gedämpften Schwingung.

Makroskopische physikalische Systeme sind immer gedämpft. Da sie beispielsweise durch Reibung Energie an die Umgebung abgeben, nimmt die Amplitude ihrer Schwingung im Laufe der Zeit ab. Überlässt man ein solches System sich selbst (freie Schwingung), so führt dieses letztendlich zum „Stillstand“, wie aus dem zweiten Hauptsatz der Thermodynamik hervorgeht. Perpetua Mobilia sind also (siehe Energieerhaltungssatz) nicht möglich.

Stellt man die Bewegungsgleichung eines Federpendels mit einer zur Geschwindigkeit proportionalen Dämpfung auf, so ergibt sich folgende Differentialgleichung:

mx¨+dx˙+kx=0{displaystyle m{ddot {x}}+d{dot {x}}+kx=0,}

Dabei ist

m{displaystyle m} die Masse,

d{displaystyle d} die Dämpfungskonstante und

k{displaystyle k} die Federkonstante.

(Für Drehschwingungen ist m{displaystyle m} durch das Trägheitsmoment J{displaystyle J} und x{displaystyle x} durch den Auslenkungswinkel φ{displaystyle varphi } zu ersetzen.)

Hierbei handelt es sich um eine homogene lineare gewöhnliche Differentialgleichung 2. Ordnung, die sich auf die allgemeine Form

x¨+2δx˙+ω02x=0{displaystyle {ddot {x}}+2delta {dot {x}}+omega _{0}^{2}x=0,}

bringen lässt, wenn man die (positiven) Abkürzungen für die Abklingkonstante

δ=d2m{displaystyle delta ={frac {d}{2m}}}

und die ungedämpfte Eigenkreisfrequenz

ω0=km{displaystyle omega _{0}={sqrt {frac {k}{m}}}}

einführt, deren Bedeutungen erst bei der Interpretation der Lösung deutlich werden.

Beim klassischen Weg zur Lösung einer solchen linearen homogenen Differentialgleichung (alternativ kann man Methoden der Operatorenrechnung benutzen) können mit Hilfe des Ansatzes

x(t)=eλt{displaystyle x(t)=e^{lambda t},}

mit gegebenenfalls komplexem Parameter λ{displaystyle lambda } zwei linear unabhängige Lösungen gefunden werden, welche ein Fundamentalsystem bilden. Eingesetzt in die Differentialgleichung ergibt sich:

(λ2+2δλ+ω02)eλt=0{displaystyle (lambda ^{2}+2delta lambda +omega _{0}^{2}),e^{lambda t}=0}.

In dieser Gleichung kann nur der Klammerausdruck gleich Null sein. Man erhält die sogenannte charakteristische Gleichung zur Bestimmung der Konstante λ{displaystyle lambda }:

λ2+2δλ+ω02=0{displaystyle lambda ^{2}+2delta lambda +omega _{0}^{2}=0}

Das ist eine quadratische Gleichung, deren Diskriminante

δ2−ω02{displaystyle delta ^{2}-omega _{0}^{2}}

bestimmt, ob sie zwei reelle Lösungen, zwei konjugiert komplexe Lösungen oder eine sogenannte Doppelwurzel besitzt. Deshalb ist eine Fallunterscheidung erforderlich.

Die Theorie der linearen Differentialgleichungen zeigt, dass die allgemeine Lösung der homogenen Differentialgleichung eine Linearkombination der beiden ermittelten Lösungen ist. Besitzt die charakteristische Gleichung zwei Lösungen (also ist die Diskriminante ungleich 0), dann lässt sich die allgemeine Lösung der Bewegungsgleichung wie folgt schreiben:

x(t)=X1eλ1t+X2eλ2t.{displaystyle x(t)=X_{1}e^{lambda _{1}t}+X_{2}e^{lambda _{2}t}.}

Die beiden (im Allgemeinen komplexen) Konstanten X1{displaystyle X_{1}} und X2{displaystyle X_{2}} repräsentieren die zwei noch vorhandenen Freiheitsgrade der allgemeinen Lösung. Durch die Festlegung von zwei Anfangsbedingungen (z. B. x(0){displaystyle x(0)} oder/und x˙(0){displaystyle {dot {x}}(0)}) müssen die beiden Konstanten für einen konkreten Fall präzisiert werden.

Schwingfall (links), Aperiodischer Grenzfall (mittig) und Kriechfall (rechts) einer gedämpften Schwingung.

Schwingfall |

Eine Schwingung kann es nur geben, wenn die Verluste gering sind. Dann ist mit δ<ω0{displaystyle delta <omega _{0}} die Diskriminante negativ, der Wurzelausdruck imaginär und man erhält zwei konjugiert komplexe Lösungen:

λ1,2=−δ±iω02−δ2{displaystyle lambda _{1,2}=-delta pm i{sqrt {omega _{0}^{2}-delta ^{2}}}}.

Mit der gedämpften Eigenkreisfrequenz:

ωd=ω02−δ2{displaystyle omega _{d}={sqrt {omega _{0}^{2}-delta ^{2}}}}.

ergibt sich kürzer:

λ1,2=−δ±iωd{displaystyle lambda _{1,2}=-delta pm iomega _{d}}.

Damit erhält man

x(t)=e−δt(X1eiωdt+X2e−iωdt).{displaystyle x(t)=e^{-delta t}left(X_{1}e^{iomega _{d}t}+X_{2}e^{-iomega _{d}t}right).}

Mit Hilfe der Eulerschen Formeln lässt sich die Lösung der homogenen Differentialgleichung auch in trigonometrischer Form angeben. In der Theorie der linearen Differentialgleichungen mit konstanten Koeffizienten^[7] wird gezeigt, dass diese (im Gegensatz zur Exponentialform) rein reell und dadurch praktisch besser interpretierbar ist:

x(t)=e−δt(X3sin⁡(ωdt)+X4cos⁡(ωdt)){displaystyle x(t)=e^{-delta t}left(X_{3}sin(omega _{d},t)+X_{4}cos(omega _{d},t)right),}

oder

x(t)=x0e−δtcos⁡(ωdt+φ0){displaystyle x(t)=x_{0},e^{-delta t}cos(omega _{d},t+varphi _{0}),}

Auch hier sind jeweils die beiden Konstanten X3{displaystyle X_{3}} und X4{displaystyle X_{4}} bzw. x0{displaystyle x_{0}} und φ0{displaystyle varphi _{0}} durch die Anfangsbedingungen zu bestimmen. Insbesondere die letzte Form ist leicht als „gedämpfte Schwingung“ zu interpretieren.

Durch Vorgabe der zwei Anfangsbedingungen x(0){displaystyle x(0)} und x˙(0){displaystyle {dot {x}}(0)} können die beiden Konstanten eliminiert werden. Ausgehend von der ersten trigonometrischen Form erhält man die konkrete von beiden Anfangsbedingungen abhängige Lösung

x(t)=e−δt(x˙(0)+δx(0)ωd⋅sin⁡(ωdt)+x(0)⋅cos⁡(ωdt)).{displaystyle x(t)=e^{-delta t}left({frac {{dot {x}}(0)+delta x(0)}{omega _{d}}}cdot sin(omega _{d},t)+x(0)cdot cos(omega _{d},t)right),.}

Wenn die Abklingkonstante δ{displaystyle delta } gleich Null ist, bleibt die Amplitude konstant. Die Schwingung ist ungedämpft mit der Kreisfrequenz ωd=ω0{displaystyle omega _{d}=omega _{0}}.

Aperiodischer Grenzfall |

Die Grenze, ab der keine Schwingung mehr möglich ist, bildet der aperiodische Grenzfall (δ=ω0{displaystyle delta =omega _{0}} bzw. ωd=0{displaystyle omega _{d}=0}). Die Lösung enthält dann keine Sinusfunktion. Da nun λ1=λ2=−δ{displaystyle lambda _{1}=lambda _{2}=-delta } gilt, muss eine zu eλ1t{displaystyle e^{lambda _{1}t}} unabhängige zweite Lösung auf andere Weise konstruiert werden. Es ergibt sich

x(t)=X1e−δt+X2te−δt.{displaystyle x(t)=X_{1}e^{-delta t}+X_{2}te^{-delta t}.}

Kriechfall |

Bei hoher Dämpfung, also für δ>ω0{displaystyle delta >omega _{0}} ergibt sich der Kriechfall, dessen Lösung sich aus zwei Exponentialfunktionen mit den beiden reellen λ1,2{displaystyle lambda _{1,2}} zusammensetzt:

x(t)=X1eλ1t+X2eλ2t{displaystyle x(t)=X_{1}e^{lambda _{1}t}+X_{2}e^{lambda _{2}t}}.

Frequenzspektrum einer Schwingung |

Zusammenhang von Zeit- und Frequenzbereich

Eine Schwingung lässt sich statt als zeitabhängige Änderung auch als Funktion im Frequenzraum betrachten. Die mathematische Transformation nennt man Fouriertransformation. Der Informationsgehalt bleibt dabei erhalten, daher lässt sich aus einem Frequenzspektrum durch Rücktransformation immer die entsprechende zeitabhängige Schwingung rekonstruieren. Hintergrund dieser Überlegung ist, dass sich jede Schwingung durch eine additive Überlagerung (Superposition) von harmonischen Schwingungen unterschiedlicher Frequenz darstellen lässt. Die Superposition zweier harmonischer Schwingungen nennt man Schwebung.

Anregung einer Schwingung |

Freie Schwingungen |

Freie Schwingungen führt ein schwingfähiges System aus, das – nach einer Störung/Auslenkung sich selbst überlassen – je nach Dämpfung oszillierend oder „kriechend“ in den Gleichgewichtszustand zurückkehrt (siehe oben). Die Frequenz der freien Schwingung ist die Eigenfrequenz des Schwingers. Bei Schwingungen mit mehreren Freiheitsgraden gibt es entsprechend viele Eigenfrequenzen.

Erzwungene Schwingungen |

Erzwungene Schwingungen führt ein Schwinger aus, der durch zeitveränderliche äußere Einwirkung zum Schwingen angeregt (gezwungen) wird. Praktisch bedeutsam sind vor allem periodische Erregungen und darunter die harmonische, sinusförmige Erregung. Die Frequenz der periodischen Erregung wird als Erregerfrequenz bezeichnet. Es gibt auch mehrfrequente Erregungen oder Erregungen durch Zufallsprozesse.

Im Falle der harmonischen Erregung führt ein lineares System im Allgemeinen zwei Schwingungen gleichzeitig aus:

• die freie Schwingung (mit der Eigenfrequenz bzw. mehreren Eigenfrequenzen), deren Größe von den Anfangsbedingungen abhängt und die durch die stets vorhandene Dämpfung während der Einschwingzeit abklingt und


• die erzwungene Schwingung mit der Erregerfrequenz bei konstanter Anregungsstärke. Die Amplitude dieser Schwingung ist nach Beendigung des Einschwingvorgangs konstant. Das Verhältnis zwischen der Amplitude und der Stärke der Erregung wird durch die Vergrößerungsfunktion quantifiziert.

In der Technischen Mechanik sind die wichtigsten Erregungsmechanismen die Wegerregung, die Krafterregung und die Unwuchterregung (siehe Vergrößerungsfunktion).

Die Amplitude der erzwungenen Schwingung nimmt im Falle der Resonanz ein Maximum an. Bei fehlender Dämpfung und Gleichheit von (einer) Erregerfrequenz und (einer) Eigenfrequenz wird die Amplitude unendlich. Mit wachsendem Dämpfungswert verschiebt sich die Resonanzstelle geringfügig und die Resonanzamplitude nimmt ab.

Selbsterregte Schwingungen |

Schwingungssysteme, bei denen die Energiezufuhr durch ein geeignetes Steuerelement und den Schwingungsvorgang selbst gesteuert wird, führen selbsterregte Schwingungen aus und werden Oszillator genannt. In den Differentialgleichungen wirkt sich diese Erscheinung so aus, dass der Dämpfungswert Null wird. Ein typisches Beispiel im Bereich der Mechanik sind die Schwingungen der Saiten einer Violine. Diese werden dadurch verursacht, dass die Haftreibung zwischen Bogen und Saite größer ist als die Gleitreibung und die Gleitreibung mit wachsender Differenzgeschwindigkeit noch abnimmt. Weitere Beispiele sind das Tönen von Gläsern durch Reiben des Randes und elektronische Taktgeber (Oszillatorschaltung).

Selbsterregte Schwingungen nehmen in der Amplitude zu, bis die überproportional mit der Amplitude zunehmende Dämpfung die Energieeinkopplung kompensiert oder das schwingende System zerstört wird.

Parametererregte Schwingungen |

Eine parametererregte Schwingung tritt dann auf, wenn sich Parameter des Schwingungssystems (Trägheitsgrößen, Dämpfungswerte oder Federkonstanten) periodisch ändern, z. B. beim Schaukeln.

Lineare und nichtlineare Schwingungen |

Lineare Schwingungen sind dadurch gekennzeichnet, dass sie sich mit Differentialgleichungen beschreiben lassen, bei denen alle Abhängigkeiten von der schwingenden Größe und ihren zeitlichen Ableitungen linear sind. Bei nichtlinearen Schwingungen ist dies nicht der Fall, sie sind daher nicht streng sinusförmig. Von größerer praktischer Bedeutung ist, dass sich bei einem getriebenen Oszillator das Resonanzverhalten erzwungener Schwingungen ändert und die Amplituden selbsterregter Schwingungen beschränkt bleiben.

Nichtlineare Systeme sind häufig nicht integrabel, d. h. die Differentialgleichung(en) besitzen keine analytische Lösung. Das Schwingverhalten solcher Systeme wird daher meist mit numerischen Computersimulationen untersucht. Eines der ersten dieser Experimente war das Fermi-Pasta-Ulam-Experiment, bei dem eine Saitenschwingung mit nichtlinearem Störterm untersucht wurde. Als Lösung solcher Systeme erhält man je nach Energie der Schwingung häufig eine quasiperiodische oder chaotische Oszillation. Chaotisches Verhalten lässt sich beispielsweise bei einem Doppelpendel beobachten. Ein nichtlineares System, das kein chaotisches Verhalten ermöglicht, ist der Van-der-Pol-Oszillator.

Schwingungen mit mehreren Freiheitsgraden |

Diese Animation zeigt eine Lissajous-Figur, wie sie ein Oszilloskop, bei einem Frequenz-Verhältnis von annähernd 2:3 anzeigen würde (Amplituden-Verhältnis 1:1)

Schwingungen mit einem Freiheitsgrad sind solche, die sich mit einer schwingenden Größe vollständig beschreiben lassen. Ein Beispiel dafür sind Schwingungen des ebenen Fadenpendels. Lässt man beim Pendel räumliche Bewegungen zu wie bei einem foucaultschen Pendel, so handelt es sich bereits um einen Schwinger mit zwei Freiheitsgraden. Im Folgenden beschränken wir uns auf die Betrachtung kleiner Auslenkungen.

An diesem Beispiel lässt sich sehen, dass die Bezeichnung als Schwingung von den betrachteten Größen abhängen kann, also der Wahl der generalisierten Koordinaten. So lässt sich das Pendel auslenken, sodass die Schwingung in einer Ebene stattfindet. Gibt man dem Pendel zusätzlich noch eine Anfangsgeschwindigkeit senkrecht zur Auslenkungsrichtung, so kann man Ellipsenbahnen oder eine Kreisbewegung mit konstanter Winkelgeschwindigkeit beobachten.

Betrachtet man Auslenkungswinkel des Pendels von der Seite von zwei verschiedenen Richtungen, erhält man zwei harmonischen Schwingungen gleicher Periodendauer. Eine Überlagerung von zwei harmonischen Schwingungen nennt man Lissajous-Figur. Eine andere Möglichkeit ist, das Pendel von oben zu betrachten und Abstand zur Ruhelage sowie die Richtung der Auslenkung als fortlaufende Entfernung zum Anfangswinkel zu notieren. Im Fall einer Kreisbahn sind beide keine Schwingungen mehr.

Die Anzahl der Freiheitsgrade eines mechanischen Systems mit mehreren Massen, die sich unabhängig voneinander bewegen können, ist die Summe aller einzelnen Freiheitsgrade. Weitere Beispiele für Schwingungen mit mehreren Freiheitsgraden sind Torsionsschwingungen einer Kurbelwelle oder die Horizontalschwingungen eines mehrgeschossigen Bauwerkes unter Erdbebeneinfluss.

Manche Schwingungen eines Systems mit mehreren Freiheitsgraden lassen sich bei geeigneter Wahl der Koordinaten als mehrere unabhängige Schwingungen betrachten. Für eine Schwingung, die sich mittels Differentialgleichungen beschreiben lässt bedeutet dies, die Gleichungen der einzelnen Koordinaten zu entkoppeln. Sind die einzelnen Schwingungen periodisch, lassen sich dann aus den entkoppelten Differentialgleichungen die Eigenfrequenzen des Systems bestimmen. Lassen sich alle Eigenfrequenzen als ganzzahliges Vielfaches einer Konstanten schreiben, so ist auch die Schwingung des Gesamtsystems periodisch.

Bei nichtlinearen Schwingungssystemen ist eine Entkopplung der Differentialgleichungen in geschlossener Form meist nicht möglich. Es existieren jedoch Näherungsverfahren, die ausgehend von einer Linearisierung der Differentialgleichungen eine iterative Lösung ermöglichen.

Schwingungen eines Kontinuums |

Schwingungen quadratischer Platten. Dargestellt sind die Knotenlinien von stehenden Wellen, auch Chladnische Klangfiguren genannt.

Eine an einer Stelle in einem Kontinuum angeregte Schwingung breitet sich darin als Welle aus. An Grenzflächen, an denen das Ausbreitungsmedium wechselt, kann die Welle reflektiert werden. Innerhalb des schwingenden Körpers überlagern sich die ursprüngliche und die reflektierte Welle, so dass eine stehende Welle entsteht; Beispiele sind eine schwingende Saite eines Musikinstruments – geometrisch eindimensional – oder die zweidimensional schwingende Membran in einem Lautsprecher. Die stehende Welle lässt sich mathematisch durch unendlich viele gekoppelte Oszillatoren, also ein System mit unendlich vielen Freiheitsgraden beschreiben.

Von praktischem Interesse in der Technik sind des Weiteren die Schwingungen von Stäben, Platten und Schalen. Ein einseitig eingespannter Balken besitzt viele Freiheitsgrade der Schwingung, die sich nicht nur durch ihre Resonanzfrequenzen, sondern auch durch die Art ihrer Bewegung unterscheiden.

• 
  

  

  
  

  
  

  Schwingungsform eines einseitig eingespannten Balkens bei der tiefsten Eigenfrequenz - erste Querbiegungsmode
  

  
  

  
  


• 
  

  

  
  

  
  

  Schwingungsform desselben Balkens bei einer höheren Eigenfrequenz - zweite Vertikalbiegungsmode
  

  
  

  
  


• 
  

  

  
  

  
  

  Schwingungsform desselben Balkens bei einer höheren Eigenfrequenz - erste Torsionsmode
  

  
  

  
  


• 
  

  

  
  

  
  

  Schwingungsform desselben Balkens bei einer höheren Eigenfrequenz - zweite Torsionsmode
  

  
  

  
  

Weitere Beispiele |

Im Alltag begegnen uns Schwingungen zum Beispiel in Musikinstrumenten und am Uhrpendel, aber auch in Schwingquarzen von Uhren oder zur Takterzeugung in anderen elektronischen Geräten.

Auch die Atome in einem Kristallgitter oder Moleküle können um eine Gleichgewichtslage schwingen und erzeugen so zum Beispiel charakteristische Absorptionsspektren.

Oszillierende Reaktionen geben den Takt vor für die Atmung und den Herzschlag.

Bei Elektronenröhren wird häufig Mikrofonie beobachtet. Sie entsteht durch von außen auf die Bauteile einwirkende störende mechanische Schwingungen etwa durch nah dabeistehende Lautsprecher.

Als Regenerativeffekt bezeichnet man in der Fertigungstechnik Schwingungen, die während des Fertigungsvorganges innerhalb einer Maschine auftreten.

In der Geologie und Meteorologie werden kleinere und mit gewisser Regelmäßigkeit wiederkehrende Schwankungen des Meeresspiegels, der Eisrandlagen, der Erdkrustenstücke, des Erdmagnetfeldes oder des Klimas beobachtet.

In der Wirtschaft dient das Goodwin-Modell zur Erklärung von Konjunkturzyklen.

Die Lotka-Volterra-Gleichungen beschreiben näherungsweise die Schwankungen von Räuber- und Beutepopulationen.

Siehe auch |

• Harmonograph


• 
  Humanschwingungen, mechanische Schwingungen, die auf den Menschen einwirken


• 
  Vibrationen, Schwingungen von Stoffen und Körpern


• Zeigermodell

Literatur |

• 
  Hans Dresig, Alexander Fidlin: Schwingungen und mechanische Antriebssysteme: Modellbildung, Berechnung, Analyse, Synthese. 3., überarb. und erw. Auflage. Springer Vieweg Verlag, Berlin / Heidelberg 2014, ISBN 978-3-642-24116-1. 
  


• N. N. Bogoliubow, Y. A. Mitropolski: Asymptotic Methods in the Theory of Non-Linear Oscillations. 2. Auflage. Hindustan Pub. Corp. / Gordon and Breach Science Publishers, Delhi / New York / London 1961, OCLC 564000480 (englisch, Inhaltsverzeichnis – eingeschränkte Vorschau). 
  


• Th. Frey, M. Bossert: Signal- und Systemtheorie. In: Teubner Informationstechnik. Teubner Verlag, Stuttgart / Leipzig / Wiesbaden 2004, ISBN 3-519-06193-7. 
  


• 
  Anatole Katok, Boris Hasselblatt: Introduction to the modern theory of dynamical systems. In: Encyclopedia of mathematics and its applications. Band 54. Cambridge University Press, Cambridge 1996, ISBN 0-521-57557-5 (englisch). 
  

Weblinks |

 Wikibooks: Schwingbewegungen – Lern- und Lehrmaterialien

 Wiktionary: oszillieren – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Schwingungen: Kurs Uni Göttingen

Einzelnachweise |

1. 
   ↑
   Kurt Magnus, Karl Popp: Schwingungen. 7. Auflage. Teubner, 2005, ISBN 3-519-52301-9, S. 13 (eingeschränkte Vorschau in der Google-Buchsuche): „Als Schwingungen werden mehr oder weniger regelmäßig erfolgende zeitliche Schwankungen von Zustandsgrößen bezeichnet.“ 
   


2. 
   ↑
   DIN 1311-1:2000: Schwingungen und schwingungsfähige Systeme – Teil 1: Grundbegriffe, Einteilung. Abschnitt 3 „Eine Schwingung ist eine zeitliche Änderung einer Zustandsgröße eines Systems, bei der im allgemeinen diese Zustandsgröße abwechselnd zu- und abnimmt. Spezielle zeitliche Änderungen wie Stoß- und Kriechvorgänge werden im erweiterten Sinn auch als Schwingungen bezeichnet.“
   


3. 
   ↑ 13 Schwingungen. (PDF; 92 kB) TU Cottbus.
   


4. 
   ↑
   Rudolf Jürgler: Maschinendynamik. 3., neu bearbeitete Auflage. Springer, 2004, ISBN 3-540-62227-6, S. 3 (eingeschränkte Vorschau in der Google-Buchsuche). 
   


5. 
   ↑ Michel Hénon: Numerical exploration of Hamiltonian Systems. Iooss, Helleman, Stora (Hrsg.): Chaotic Behaviour of Deterministic Systems. North-Holland, 1983, S. 53–76.
   


6. 
   ↑ Steven H. Strogatz: Nonlinear Dynamics and Chaos. Perseus Books, 2001, S. 273 ff., Kapitel 8.6 – Coupled Oscillators and Quasiperiodicity.
   


7. 
   ↑ Wladimir Iwanowitsch Smirnow: Lehrgang der höheren Mathematik. 8. Auflage. Band 2. Deutscher Verlag der Wissenschaften, Berlin 1968, DNB 368242544.