Tonleiter
Eine Tonleiter oder (Ton-)Skala ist in der Musik eine Reihe von der Tonhöhe nach geordneten Tönen, die durch Rahmentöne begrenzt wird, jenseits derer die Tonreihe in der Regel wiederholbar ist.[1]
In den meisten Fällen hat eine Tonleiter den Umfang einer Oktave und folgt dabei in vielen Fällen einem heptatonischen Tonskalenaufbau. Wie eine Tonleiter aufgebaut ist, wird im Tonsystem festgelegt.
Die gebräuchlichsten europäischen und außereuropäischen Tonleitern basieren auf fünf oder sieben Tönen innerhalb der Oktave, welche Tonstufen genannt werden. Weit verbreitet sind diatonische Tonleitern in Dur und Moll oder die Kirchenleitern. Tonleitern sind durch Tonabstände definiert. Die in der konkreten Tonleiter enthaltenen Töne bezeichnet man als leitereigene Töne.
In außereuropäischer Musik wie der klassischen arabischen oder indischen Musik gibt es Tonsysteme und Tonleitern, die den Tonraum anders aufteilen. So gibt es Tonleitern, die mehr als sieben festgelegte Tonstufen enthalten, wie zum Beispiel Mugam, Maqam oder Raga.
Inhaltsverzeichnis
1 Beispiel
2 Beispiele für Tonleitern
3 Bildliche Darstellung von Tonleitern
3.1 Das harmonisch-reine Tonnetz
3.2 Darstellung im temperierten Halbtonzirkel
3.3 Tastenbelegungen als Vorlage
4 Siehe auch
5 Weblinks
6 Einzelnachweise
Beispiel |

C-Dur-Tonleiter
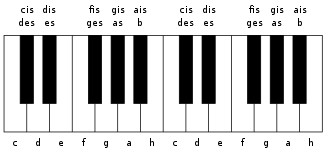
Klaviatur über zwei Oktaven
Als Beispiel eine der heute in Mitteleuropa gebräuchlichsten Tonleitern: die Dur-Tonleiter. Sie besteht aus Tönen im Abstand:
Ganzton – Ganzton – Halbton – Ganzton – Ganzton – Ganzton – Halbton
Man kann eine so definierte Tonleiter auf jedem beliebigen Ton beginnen. Durch Angabe eines konkreten Anfangstons (Grundtons) wird daraus eine Tonart wie C-Dur, D-Dur usw.
C-Dur: C-D-E-F-G-A-H-C
D-Dur: D-E-Fis-G-A-H-Cis-D
Die leitereigenen Töne von C-Dur heißen auch Stammtöne und entsprechen den weißen Tasten auf einer Klaviatur.
Auf einer Klaviatur sind den schwarzen Tasten „erhöhte“ oder „erniedrigte“ leitereigene Töne zugeordnet. Im deutschen Sprachraum werden sie erhöht Cis, Dis, Fis, Gis und Ais genannt und erniedrigt Des, Es, Ges, As und B. In anderen Kulturräumen werden die Töne mit anderen Namen bezeichnet. Heute wird in den meisten Fällen auf Tasteninstrumenten die gleichstufige Stimmung eingesetzt, somit können die Halbtöne enharmonisch ausgetauscht werden. Das heißt, auf einer Klaviatur gibt es nur eine Taste für Cis und Des, für Dis und Es usw. Somit entspricht jeder der zwölf möglichen Töne innerhalb einer bestimmten Oktave einer bestimmten Frequenz.
Beispiele für Tonleitern |
- Die Tonleitern der Pentatonik (fünf Töne):
- gewöhnliche Dur- und Mollpentatonik
- Die zwölf Lü der chinesischen Musik
- Japanische Pentatonik
- Indische Pentatonik
- der Slendro der Insel Java,
- der Pélog aus Indonesien
- Die Ganztonleiter (Hexatonik, sechs Töne)
- Die Tonleitern der Heptatonik (sieben Töne):
- Die Durtonleiter
- Die verschiedenen Molltonleitern (reines oder natürliches Moll, harmonisches Moll, melodisches Moll)
- Die Kirchentonleitern (Dorisch, Phrygisch, Lydisch, Mixolydisch, Lokrisch usw.)
- Die phrygisch-dominante Tonleiter
- Die Zigeunertonleitern
- Die Harmonisch-Dur-Tonleiter
- Die Mi-Sheberach-Tonleiter
- Die alterierte Skala
- Die enigmatische Leiter
- Die Durtonleiter
- Die verminderte Skala (Oktatonik, acht Töne, auch Ganzton-Halbton-Leiter bzw. Halbton-Ganzton-Leiter genannt)
- Die chromatische Tonleiter (zwölf Töne)
- Sonstige:
- Die frühgriechischen Aulos-Modi
- Die Ragas der indischen Musik
- Die Skalen des persischen Dastgah-Systems
- Die Bluestonleiter (siehe auch Blue Notes)
- Die Shepard-Skala
- Die frühgriechischen Aulos-Modi
Bildliche Darstellung von Tonleitern |
Es gibt unterschiedliche bildliche Darstellungen, die – je nachdem was verdeutlicht werden soll – mehr oder weniger gut geeignet sind, bestimmte Zusammenhänge zu verdeutlichen. In vielen Fällen lehnen sich die Darstellungen an den Griffmustern oder Tabulaturen von Instrumenten an. Einige wenige Darstellungen sind auch von bekannten Musiktheoretikern in deren Werken eingeführt worden, um bestimmte Theorien zu verdeutlichen. Darstellungen, die allen Aspekten gerecht werden, gibt es nicht.
Das harmonisch-reine Tonnetz |

Schema eines harmonisch reinen Tonnetzes.
Nach Leonhard Euler[2], veröffentlicht in „Novi Commentarii academiae scientiarum Petropolitanae“[3].
Es bildet nicht nur die Tonbeziehungen der harmonisch-reinen Stimmung ab (die Töne a, e und h erklingen so ein syntonisches Komma tiefer als in der pythagoreischen Quintenkette), sondern auch sehr anschaulich den Akkordvorrat einer jeden Dur- oder Molltonleiter, was insbesondere bei harmonisch und melodisch Moll sehr sinnvoll ist. Tatsächlich sind unsere geläufigen Dur- und Molltonleitern genau so gedacht, als in eine Oktave gebrachtem Tonvorrat der wichtigsten Harmonien (hier: F-Dur (links), C-Dur (mitte), G-Dur (rechts), …). Nebenharmonien eben jeweils daneben vgl.: Carl Dahlhaus „Untersuchungen über die Entstehung der harmonischen Tonalität“[4]
Zudem lassen sich mit diesem Tonnetz selbst funktionsharmonische Beziehungen verständlich darstellen; vgl.: Renate Imig: Systeme der Funktionsbezeichnung in den Harmonielehren seit Hugo Riemann[5]
Darstellung im temperierten Halbtonzirkel |

Halbtonzirkel nach Guerino Mazzola[6]
Die innere Symmetrie (hier as-d) wird sofort ersichtlich, was insbesondere bei einer Darstellung der Modi mit begrenzten Transpositionsmöglichkeiten hilfreich ist. Diese Grafik lässt sich auch auf die Darstellung von Zwölftonreihen oder Akkorden erweitern. Jedoch ist diese in dieser Fassung an einen Grundton gebunden. Man kann die Tonbuchstaben einfach weglassen, solange ersichtlich ist, wo die Skala anfängt und wo sie aufhört. Diese Darstellung setzt die gleichstufige Temperatur voraus, was bei Kirchenmodi natürlich historisch nicht korrekt ist. Man könnte aber auch anstelle des Halbtonzirkels die Quintenspirale o. Ä. verwenden. Es sieht so aus, als ob Töne übersprungen würden, und es wird nicht zwischen diatonischem und chromatischem Halbtonschritt unterschieden; das ist in jeder Darstellung, die auf der temperierten Skala basiert.
Tastenbelegungen als Vorlage |

Die folgenden Grafiken stellen verschiedene Tonleitern nach der wenig verbreiteten Tastenbelegung von 6-plus-6-Instrumenten bildlich dar.
Das nebenstehende Schema zeigt eine chromatische Tonleiter. Das unterste Kästchen stellt den Grundton dar. Die Kästchen darüber sind die Töne der Tonleiter, benannt nach ihren Intervall zum Grundton. Die „Leiter“ ist also zickzackförmig zu lesen. Das oberste Kästchen stellt denselben Ton wie der Grundton dar, nur eine Oktave höher.
Das Schema ermöglicht das Erinnern von Mustern. Die Muster sind Distanzmuster, es lassen sich Halbtonschritte, Ganztonschritte und drei Halbtonschritte leicht erkennen.
 Dur (Ionisch) |  reines Moll (Äolisch) | 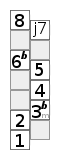 harmonisches Moll |  Zigeuner-Moll |  melodisches Moll |
 Dorisch |  Phrygisch | 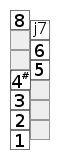 Lydisch | 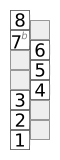 Mixolydisch | 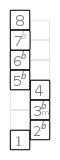 Lokrisch |
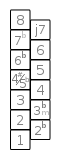 Chromatisch |  Ganztonleiter |  Dur-Pentatonik | 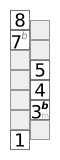 Moll-Pentatonik |  Alterierte Skala |
 Verminderte Skala, 1. Form | 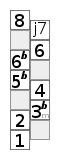 Verminderte Skala, 2. Form |  phrygisch-dominante Tonleiter (Spanische / Jüdische Tonleiter) (z. B. Hava Nagila) |  Zigeuner-Dur (Arabische Tonleiter) |  Mi Sheberach |
Siehe auch |
- Naturtonreihe
- Modale Tonleitern
- Tonleitern der griechischen Popularmusik (Laiki Dromi)
Weblinks |
- PowerPoint-Präsentation zum Erstellen von Tonleitern
- Datenbank aller 2048 möglichen Skalen in 12 Tönen im .xls und FileMaker Format, System zur Kategorisierung von Skalen
Harmonielehre-Workshop #1 – Dur Tonleiter auf bonedo.de
- Hörbeispiele:
- Alle wichtigen Tonleitern/ Erklärungen, Noten- und Hörbeispiele
- Einige Skalen mit Midi-Hörbeispielen
- Stimmungen:
Scala – Programm zum Erstellen, Analysieren und Manipulieren von Tonleitern und Stimmungen (Freeware)
Tonleitern und Skalen auf musikanalyse.net
Einzelnachweise |
↑ Willibald Gurlitt, Hans Heinrich Eggebrecht (Hrsg.): Riemann Musiklexikon. Sachteil. 12. Auflage. B.Schott’s Söhne, Mainz 1967, S. 968.
↑ Leonhard Euler: De harmoniae veris principiis per speculum musicum repraesentatis
↑ Novi Commentarii academiae scientiarum Petropolitanae 18, St. Petersburg, 1774
↑ Carl Dahlhaus: Untersuchungen über die Entstehung der harmonischen Tonalität. Kassel 1965.
↑ Renate Imig: Systeme der Funktionsbezeichnung in den Harmonielehren seit Hugo Riemann. Düsseldorf 1970.
↑ Guerino Mazzola: Geometrie der Töne. Basel 1990, S. 78, 110.